
Phyllotaxie : du Grec "Phylle" = feuille et "Taxon" = disposition, ordre. Littéralement, la "phyllotaxie"est donc l'étude de "la disposition des feuilles autour des branches". Phyllotaxie "spirale" car dans la plupart des cas les feuilles s'insèrent en spirale le long de la tige.
La phyllotaxie est une théorie qui propose l´idée d´une croissance ordonnée dans le méristème
de la tige d´une plante. D´après cette théorie les feuilles apparaissent suivant une séquence
définissant divers types de disposition d´ensemble. Il existe 3 grands critères caractérisant les
phyllotaxies:
1-
La valeur de la divergence séparant 2 feuilles successives (ou écart
angulaire).
2- Parastiques de contact ou spirales le long desquelles les feuilles suivent leur croissance.
Mais en plus, il existe plusieurs types de phyllotaxies, par mis lesquelles on distingue deux
grandes catégories (en omettant bien sur tous les intermédiaires entres elles) de dispositions:
A-Dispositions verticillées (feuilles naissent au même nœud de la tige, en anneau), absence
de spirales dans ce type de croissance. Naguère, Marie et Robert Snow ont démontré que si l´on
incise l´apex à une plante à croissance verticillée, on observe une croissance spiralée ;
B-Dispositions spiralées, les plus répandues et qui seront le type de phyllotaxie étudié dans
ce T.P.E. En une idée résumée, des feuilles apparemment isolées peuvent être reliées par une
spirale dite ontogénique (reliant les feuilles en ordre d´apparition) et n spirales dites parastiques
reliant les feuilles à n par n (exemple: 3spirales parastiques relient les feuilles de 3 en 3). Un de
ces groupes de parastiques correspond aux hélices foliaires.
Remarque:
il existe ce que l´on appel l´indice de phyllotaxie, qui correspond aux nombre
n de
tours
en hélice que l´on doit poursuivre pour retrouver un point à la même
position par rapport à
une
droite donnée, parallèle à l´axe de rotation de cette hélice (voir passage
entre les points
Violets
sur la FIGURE 4).
Recherche d´une disposition optimale.
Lors de la
croissance des bourgeons chez une plante, ceux-ci cherchent une position
appelée
position optimale, d´où ils peuvent croître le plus indépendamment possible
sans gêner
les
autres et sans être gêné (avoir accès à la lumière, les minéraux de l´eau,
etc…). Ils cherchent
respecter
les trois grands critères énoncés dans la définition sur la phyllotaxie.
1-Angle
de divergence optimal.
Pour trouver cet angle de divergence nous
commençons par considérer un cercle déroulé en un segment [AB] de longueur 1
et tel que A est pour angle 0° et B est pour angle 360°. Nous
nommons
C le premier organe naissant après A et B. Il est nécessaire que C apparaisse
le plus
loin
des deux points, sans pouvoir le placer au milieu, car sinon les nouveaux
bourgeons
naîtraient
sur A et B car l´angle de divergence serait de180°, ne laissant que ces 3
positions
disponibles
(voir remarque sur FIGURE 3).
Pour éviter ce problème de symétrie il faut donc
décaler
C un peu vers A ou vers B. Soit alors D le point d´une nouvelle naissance après
C entre
B
et C, si nous avons décalé C en première instance vers A. D est tel que CD=CA
(nous
cherchons
bien que les feuilles naissent le plus éloignées les unes des autres), tout en
étant pas
trop
près de B.
FIGURE
1.

Pour
que la disposition soit idéale, il faudrait que les 4 points soient équidistants
les uns des
autres,
ce qui se traduit par le fait qu´il nous faut que:
BD/BC=AC/AB
Puisque
AC=AB-BC, on a:
BD/BC=(AB-BC)/AB
Et
avec AB=1, on a:
BD/BC=1-BC
En
sachant que BD=BC-DC et CA=CD:
(BC -CA)/BC=1-BC
AC=AB-BC,
donc:
(2BC-1)/BC= 1-BC
2-(1/BC)=1-BC
BC+1-(1/BC)=0
On
multiplie par BC:
BC2+BC-1=O
D´où,
nous cherchons les deux racines BC=0,61803…, et BC´=-1,61803… (nombre d´or).
Lorsque
nous rapportons ceci au cercle dans le quel nous travaillons, on a deux angles
complémentaires:
137,5°pour
BC et 222,5°pour BC´
Ce
calcul montre donc que l´angle de divergence optimal pour la disposition des
bourgeons
en
croissance chez une plante est de 137,5°
environ. Il nous reste maintenant à trouver les
facteurs
qui influencent physiquement cet angle.
Pour
expliquer comment chaque primordia (éléments botaniques non différenciés,
pouvant
donner
naissance à une feuille, fleur, tige, etc…) sait où se trouve la plus grande
place disponible
dans
la tige, le mathématicien Alan Turing à poser pour hypothèse le fait que
chaque primordia
produisait
une substance empêchant la naissance d´autres à sa périphérie. Nous pouvons
donc
penser
qu´un nouveau primordia n´apparaît que lorsque la tige présente suffisamment
d´espace
pour
qu´il ne se gêne pas avec d´autres primordia, on voit encore l´idée de
disposition optimale.
En
simulant numériquement l´apparition des primordia S. Douady et Y. Coudier ont
démontré
que
l´angle de divergence était très dépendant d´un facteur qu´ils ont nommé G, tel que:
G=vT/Ro
Avec:
v=vitesse
d´éloignement des primordia par rapport à l´apex
T=période
d´apparition des primordia
Ro=rayon
d´apparition des primordia
Ils
ont de même remarqué que G
possédait une valeur limite
à partir de laquelle l´angle de
divergence
était égale à 180°, c´est lorsque G>0,7.
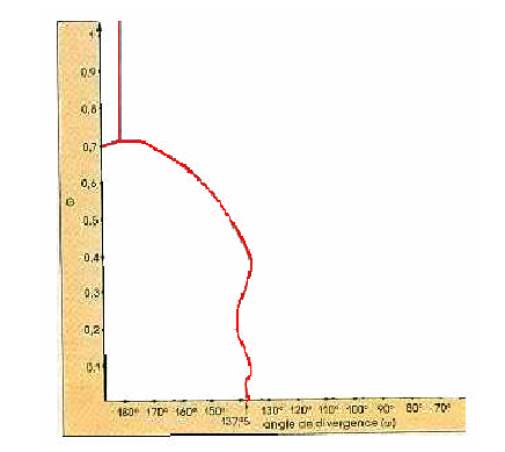
Nous pouvons le voir dans le graphique cidessous,
exprimant
l´angle de divergence en fonction de G:
FIGURE
2.
Nous
avons:
-Pour
G>0,7; chaque nouveau primordia ne ressent l´influence que d´un
autre primordia
(angle
de divergence de 180°).
-À
partir de G=0,7; chaque nouveau primordia ressent l´influence de deux autres
primordia
(angle
de divergence<180°).
-Au
fur et à mesure que G diminue,
chaque nouveau primordia ressent l´influence de
plusieurs
autres primordia (angle de divergence tend vers 137,5° lorsque l´influence des
primordia
augmente). Nous pouvons résumer tout ceci avec l´aide du schéma suivant:
FIGURE
3.
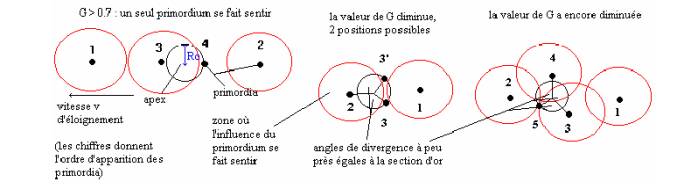
Remarque:
- le premier primordia est appelé primordium.
-On observe que la première représentation
correspond à l´exemple du cercle
déroulé
démontrant la valeur optimale de l´angle de divergence (voir FIGURE
1). Dans ce cas de
figure
on remarque bien que le point C du premier exemple ne pouvait se situer au
milieu de
[AB],
car il s´agit de l´apex. C´est ce que l´on appel brisure de symétrie.
De
même on s´est rendu compte que pour atteindre l´angle de divergence optimale,
il était
nécessaire
que G diminue graduellement et non brusquement. Dans de conditions
normales ce
phénomène
de décroissance graduée a lieu, mais il est possible de trouver des
exceptions. Ces
exceptions
sont liées à des facteurs de l´environnement extérieur et non aux
dispositions initiales
de
la plante elle- même.
2-Parastiques
de contact ou spirales montrant la chronologie de la croissance des feuilles.
Lorsque
l´on observe une plante l´organisation des grains d´une plante, on remarque
deux
grands
réseaux d´organisation de croissance, dextres ou sénestres, sans que ceci définisse
la
nature
du réseau. Il est courant de dire que c´est une phyllotaxie de type (p,q), p
et q étant des réels correspondant aux nombres de parastiches (ou spirales)
observés dans un sens comme dans l´autre (p>q; on note toujours en premier
le plus grand nombre de parastiches dans la notation).
Dans
chaque arrangement il y a toujours ce que l´on appel la spirale fondamentale
(ou spirale
ontogénique)
qui suit l´apparition des primordia un par un, et plusieurs autres spirales
dites parastiches, qui eux définissent d´autres ordres de croissance en
chronologie, bien sur en sautant
des
primordia.
Les frères
Bravais ont réussit à démontrer que puisque la divergence chez les grains d´une
plante
était égale à la section d´or, alors le nombre de parastiches correspondait
à un des nombres
appartenant
à la suite de fibonacci .
FIGURE
4.
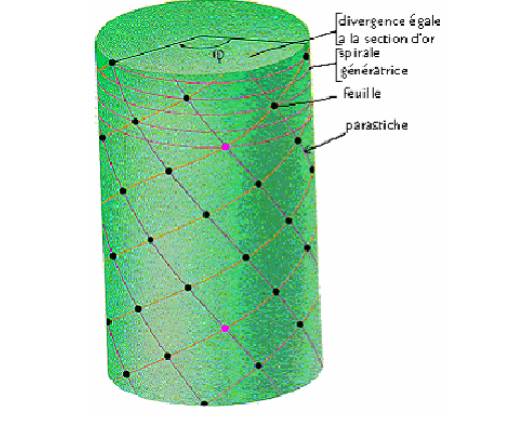
Il
faut dire que la nature des spirales prisent en compte varie d´une plante à l´autre,
et rappeler
qu´il
existe une équivalence mathématique entre les spirales (courbe dans un plan)
et les hélices
(courbe
équivalente dans l´espace), ce qui permet d´étudier la phyllotaxie soit dans
un plan ou
dans
l´espace, selon l´approche que l´on a besoin.
Disposition
verticillée
-
Le
critère de Marie et Robert Snow selon lequel un nouveau primordium apparaît dès
qu'il s'est formé un espace libre de taille suffisante. Ce critère a
l'avantage d'expliquer le mode spiralé et le mode verticillé.
Prenons
le cas d'une plante verticillée où les feuilles poussent par paires
opposées, l'apex ressemble alors à ceci :

et
en grandissant selon le critère Snow on obtient ceci :

D'où
la formation de paires de feuilles. Mais si on incise l'apex, il se produit un décalage
dans la disposition et comme l'a expérimenté le couple Snow, on obtient une
plante spiralée, ce qui montre bien que la disposition des feuilles en
verticille ou en spirale n'est pas inscrite dans les gènes. Pour expliquer
comment chaque primordium connaît quelle est la plus grande place disponible ou
quand la place est de taille suffisante, la mathématicien Alan Turing a émis
l'hypothèse que chaque primordium émet autour de lui une substance inhibitrice
empêchant la formation d'autres primordia à sa périphérie.
Disposition
spiralée
On
parle de "divergence" de la feuille pour décrire l'écartement
angulaire entre deux feuilles successives sur la tige, mesuré par une hélice
allant de la racine de la plante jusqu'à son sommet.
On
dessine une hélice passant par l'extrémité de chaque feuille jusqu'à
retrouver l'extrémité exactement verticale à la première.
Remarque : une autre façon d'interpréter ces fractions est qu'elles représentent
le nombre de tours nécessaires pour monter à la feuille suivante: un demi
tour, un tiers de tour etc...
|
|
|
|
p/q
= 2/5 |
p/q
= 3/8 |
En
fait ces fractions sont les convergentes de la fraction continue 1 -
1/(1+1/(1+1/(1+...
Si on prolonge cette fraction continue à l'aide d'un nombre infini de termes,
elle converge vers Φ'²….
De
plus le cas spiralé présenté précédemment représente plus de 90%
des plantes vivant sur notre planète.
Conclusion :
Pour conclure nous pouvons dire que la présence des suites de Fibonacci et donc du nombre d'or dans la phyllotaxie des plantes a suscité de nombreuses investigations et tentatives d'éclaircissement.
Les deux explications les plus pertinentes sont les suivantes :
1ère explication : (déjà signalée plus haut) : "Si les feuilles (et par conséquent les rameaux) d'une plante étaient espacées sur la tige par des intervalles d'exactement 137° 30' 28", aucune feuille ne se situerait exactement au-dessus d'une autre, ce qui diminuerait l'ombre portée par cette feuille sur les autres situés plus bas" (Bell, 1993, p. 222).
Il y a donc là une première régle d'optimisation de la collecte des photons, optimisation qui pourrait s'être mise en place au cours de l'évolution (i. e. les plantes présentant ce fameux décalage de l'angle d'or entre deux feuilles successives étant avantagées et donc "sélectionnées" au cours de l'évolution).
2ème explication : Le nombre d'or est lié à une spirale logarithmique.
Ainsi la question est la suivante:
pourquoi observe-t-on des spirales logarithmiques chez les plantes ?
La réponse tient à l'organisation même des cellules au coeur d'un méristème, ou, pour des plantes comme les Composées, à l'organisation des fleurons au coeur d'un capitule, etc. Dans ces deux cas (mais il y en a beaucoup d'autres : tubercules, pommes de pin, etc.) il s'agit d'un problème d'auto-organisation d'éléments tous semblables par leur forme (petites sphères pour les cellules, petits cylindres pour les fleurons) mais qui sont répartis selon un gradient de taille croissante entre le centre et la périphérie :
|
C
27 Coeur de Marguerite
|
Par exemple, dans le cas du coeur de la Marguerite (fig. phyllotaxie7 ) ou du Tournesol (fig. C 27), les fleurons ont tous la même forme (ce sont de simples tubes de section circulaire), mais pas la même taille : les plus petits sont au centre, les plus vieux à la périphérie et il existe un gradient de taille entre ces deux extrêmes. Etant tous "coincés" dans un espace restreint (ici le capitule), ils s'auto-organisent au fur et à mesure de leur croissance selon des spirales logarithmiques centrifuges, seule disposition qui permet de tenir compte (1) du changement progressif de taille sans changement de forme et (2) de la nécessité d'occuper au mieux l'espace disponible, nécessairement restreint. Dans le cas de la Marguerite, on peut compter 21 spires dans le sens des aiguilles d'une montre et 34 dans le sens inverse. Ces deux nombres appartiennent aux séries de Fibonacci et leur rapport, 1,61904..., est très proche du nombre d'or (1,61803..).
On peut faire les mêmes
observations sur une pomme de pin (FP = 8/13), les éléments modulaires qui
changent de taille sans changer de forme étant alors les écailles :
Zoom
Pomme de pin, 8/13

Une spirale logarithmique
peut s'étendre indéfiniment vers l'extérieur ou vers l'intérieur.
Elle garde donc toujours la même forme, indépendamment de sa dimension. La
forme est conservée, quelle que soit la taille. C'est d'ailleurs l'une des
raisons pour lesquelles on trouve les spirales autant représentées dans les
structures fractales, qui sont des structures "invariantes d'échelle"
(i.e. quelle que soit la "distance" à laquelle on les observe, ces
structures ont toujours la même forme).
On voit donc que lorsque
les éléments tous semblables d'une structure modulaire grandissent sans
changer de forme, les restructurations permanentes qu'ils subissent pour
minimiser les contraintes de compression tendent à les organiser le long de
spirales logarithmiques. Sachant que ces spirales sont intimement liées à la série
de Fibonacci, il n'est donc pas étonnant de constater que la phyllotaxie
spirale suit les rêgles de proportionnalité du nombre d'or
Nous
pouvons finalement conclure en disant que notre observation nous a revelé que
toutes
les plantes, d´une façon ou de l´autre cherche la disposition la plus équirépartie
entre ces
grains
le long de leur croissance, question de « coexistence » (espace pour recevoir
de la lumière,
des
minéraux à travers l´eau, pour germer dans le cas d´une fleure, ou de subir
une photosynthèse
dans
le cas d´une feuille…).